Le Tétraèdre
- Détails
- Catégorie parente: Plans de Cerfs-Volants
- Mis à jour le vendredi 6 décembre 2013 10:04
- Écrit par Josselin Millecamps - Webmaster
 Le tétraèdre est constitué de 4 faces qui sont 4 triangles équilatéraux.
Le tétraèdre est constitué de 4 faces qui sont 4 triangles équilatéraux.
Le cerf-volant tétraédrique ne ressemble à aucun autre, mais est classifié le mieux come un cerf-volant composé à dièdre, qui se compose d’un nombre (parfois un grand nombre) de cellules identiques, chacun d’un dièdre important. (Au commencement je l’ai classifié comme cerf-volant cellulaire mais j’ai changé d’avis. Ce n’est pas impossible que je puisse changer d’avis une fois de plus !)
Le cerf-volant tétraédrique était inventé par Alexander Graham Bell, mieux connu pour son autre invention, le téléphone. Quelques uns ont suggéré qu’il a du se concentrer aux cerfs-volants pour épargner le monde à un vrai fléau. En fait, le téléphone a précédé ses expériences cervolistique et a fourni les fonds aux dernières.
Le cerf-volant de Bell, souvent connu comme le Tétra, est un vrai spectacle. De plus, avec un bon vent il est très stable à cause du fort contenu dièdrique de la structure. Néanmoins, la charpente étendue et l’angle aigu de l’air des surfaces soulevantes aboutirent en un angle de vol bas.
Une autre caractéristique insolite du tétra est qu’on peut le faire en n’importe quelle taille en ajutant un nombre de cellules identique. Une seule cellule est un voleur mauvais, mais un de 4 cellules n’est pas mal, alors que c’est un peu branlant. En fait, plus on ajoute les cellules, plus sa performance améliore.
En 1907, Bell a construit un cerf-volant tétraédrique qu’il a baptisé le « Cygnet », qui se disposait de 3393 cellules, fournit de plus d’une ouverture au centre afin de porter un homme. Muni de flotteurs et tiré par un bateau à vapeur, il a beau volé pour 7 minutes au-dessus de Baddock Bay, Nouvelle Ecosse, en portant Thomas Selfridge de l’armé US. L’atterrissage a eu si douce que, son vue obscuré par l’armature toute autour de lui, il a ignoré le fait jusqu’à ce que le cerf-volant à touché la mer. Malheureusement, on n’a pas relâché la ligne de la remorque assez vite et le cerf-volant s’est détruit en se traînant à travers de l’eau. Malgé tout, Selfridge s’en est tiré seulement en se faisant bien trempé.
Le truc le plus difficile en la construction d’un tétra est comment se joindre les baguettes, les uns aux autres. Des articulations de trois types différentes sont requis, et s’ils sont conçus d’une façon particulière, il est possible à plier l’armature complète en forme plate - un avantage considérable pour la transportation.
Construire un tétra, paraîtra-t-il peut-être une tâche formidable, en fait, vous pouvez très facilement en bâtir un vous-même, de pailles et de papier cadeaux en mylar, en tous, réunis par du scotch. Un tétra plus solide, fabriqué de baguettes rigides et de tuyauterie plastique pour les jointures, est peu plus difficile, si c’est quelque peu plus coûteux et demande plus de temps. Une autre méthode de construction intéressante est offerte par Eden qui se dispose de soutien interne pour les cellules. Cependant, ce ne permet pas l’écroulement du cerf-volant pour la transportation. Voici un cliché d’un des tétra d’Anthony Thyssen.
Structure :
baguettes de 5 ou 6mm de hêtre, de ramin, d'aluminium ou de fibre de verre. 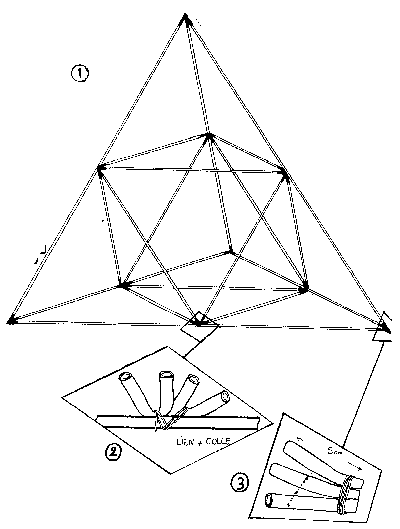
Voilure :
spinnaker, Tyvek, Nylon, plastique.
Le modèle de la photo N°1 est en toile de spinnaker.
Couper 6 baguettes de 1 m de long et 9 baguettes de 0,50 m.
Assembler selon le croquis avec des pièces de tuyau plastique (durite). Les tuyaux sont attachés par ficelle et colle (2, 3).
La structure obtenue est en fait 4 tétraèdres reliés par leurs sommets pour former un grand tétraèdre.
La voilure est constituée de 4 voiles habillant chacune 2 faces des petits tétraèdres (4).
Les côtés sont ourlés pour former une gaine permettant le passage des baguettes (1 cm environ).
Monter selon le croquis (5). La bride est en 2 points sur 2 sommets (6).

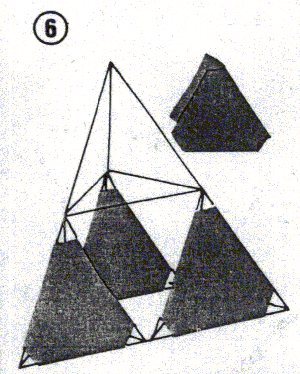

Le tétraèdre vole sommet en bas comme ci dessous :
(à la seule différence qu'ici une variation a été faite en démultipliant les tétraédres....)

Le démontage peut s'effectuer partiellement. On ne retire que les baguettes d'une face, on obtient alors deux grands triangles se rabattant l'un sur l'autre.
Sur le même principe on pourra réaliser des tétraèdres de grande dimension en multipliant les modules.
Une variation de structure est aussi possible voir figure 4 ci dessous :
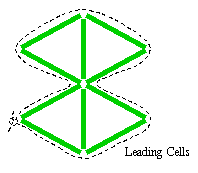
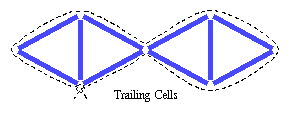
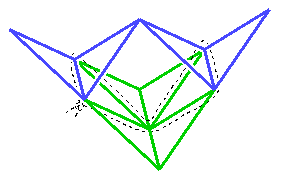
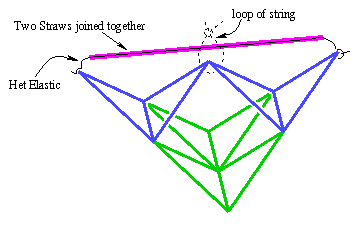
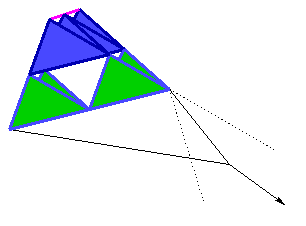
Variations sur la base du tetraédre :
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p00.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p01.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p02.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p03.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p04.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p05.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p06.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p07.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p08.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p09.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p10.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p11.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p12.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p27.gif)
Voir aussi :
Bell Tetraeder (allemand)
Bell Tetraeder 16 (allemand)
Tetrahedral (anglais)
Tetrahedral using Straws (anglais)





![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p13.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p15.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p16.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p24.gif)
![[photo]](http://www.cit.gu.edu.au/%7Eanthony/kites/tetra/100cell/p26.gif)
